Εισαγωγή

Ο Ελληνικός Αριθμός Φορολογικού Μητρώου Α.Φ.Μ. ή αλλιώς Αριθμός Φορολογικής Ταυτότητας (Α.Φ.Τ.), στα Αγγλικά Tax Identification Number (T.I.N.), είναι απαραίτητός για πολλές συναλλαγές των πολιτών (φυσικών προσώπων) και εταιριών ή οργανισμών (νομικές οντότητες) κυρίως με το κράτος αλλά όχι μόνο. Είναι μοναδικός και ακολουθεί τον κάτοχο του από την έκδοση μέχρι το θάνατο ή από την έναρξη μέχρι την παύση για νομικές οντότητες.

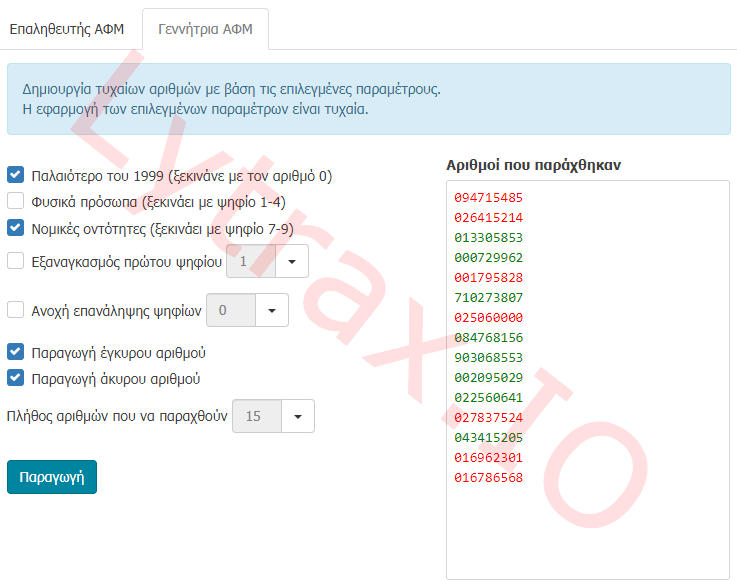
Demo

Παραγωγή έγκυρων αριθμών

Παραγωγή άκυρων αριθμών

Online εργαλείο επαλήθευσης και παραγωγής αριθμών

https://lytrax.io/blog/tools/online-greek-tin-validator-generator

Γιατί;

Πρόσφατα, έτυχε να χρειαστώ επαλήθευση για αριθμούς φορολογικού μητρώου για ένα test suite που θα έπρεπε να συνοδεύεται και από το κατάλληλο mock object που θα δημιουργούσε εικονικούς εγκύρους και άκυρους αριθμούς. Ψάχνοντας στο διαδίκτυο, το μόνο που κατάφερα να βρω σχετικά με τη δομή και τον αλγόριθμό του αριθμού, ήταν ένα άρθρο στο epixeirisi.gr με τίτλο «Αριθμός Φορολογικού Μητρώου» το οποίο περιείχε πληροφορίες με τον αλγόριθμο που γίνεται η επαλήθευση των αριθμών. Ούτε ένα επίσημο έγγραφο του κράτους σχετικά με το θέμα. Επίσης, η Ευρωπαϊκή Ένωση έχει δικό της επαληθευτή που υποστηρίζει ΑΦΤ πολλών ευρωπαϊκών χωρών συμπεριλαμβανομένης και της Ελλάδας. Ο επαληθευτής βρίσκεται σε αυτόν τον σύνδεσμο https://ec.europa.eu/taxation_customs/tin/. Στον ίδιο ιστότοπο κατάφερα να βρω ένα έγγραφό με τίτλο «∆ομή και Περιγραφή του ΑΦΤ» που περιγράφει τη δομή των ΑΦΤ για όλες τις χώρες, αλλά όταν φτάνουμε στην Ελλάδα, βλέπου μία απλή επεξήγηση ότι περιέχει 9 ψηφία και «σχόλιο: ουδέν»!

Europa EU Greek TIN Specs

Επαλήθευση

Αλγόριθμος επαλήθευσης

Ο αλγόριθμός επαλήθευσης που βρήκα στο epixeirisi.gr μου ήταν αρκετός για να προχωρήσω και να δημιουργήσω των επαληθευτή. Για να δούμε εάν ένας αριθμός είναι έγκυρος, πρέπει πρώτα να αθροίσουμε το γινόμενο κάθε αριθμητικού χαρακτήρα επί 2 υψωμένο εις το 8 μείον την θέση του χαρακτήρα με βάση το 0. Στη συνέχεια παίρνουμε το υπόλοιπο της διαίρεσης του αθροίσματος με το 11 και αν αυτό ισούται με το τελευταίο αριθμητικό ψηφίο, τότε έχουμε έγκυρο αριθμό, αλλιώς ο αριθμός είναι άκυρος. Ένας τελευταίος υπολογισμός είναι το υπόλοιπο της διαίρεσης του προηγούμενου υπολοίπου με το 10 και αυτό το κάνουμε για περιπτώσεις με αποτελέσματα μεγαλύτερα του 9.

Ο μαθηματικός τύπος του αλγόριθμού:

$$valid \iff (\biggl(\left(\displaystyle\sum_{i=0}^{7} 2^{8-i} n(i)\right) \bmod 11\biggr) \bmod 10) \sim n(8)$$

Βλέπουμε ότι ο αλγόριθμος χωρίζεται σε τέσσερις φάσεις (παρενθέσεις) όπως τις περιγράψαμε παραπάνω. Το περίπλοκο κομμάτι αφορά τον υπολογισμό του αθροίσματος ανά ψηφίο για τα πρώτα 8 ψηφία. Πρόκειται για έναν βρόγχο ο οποίος αθροίζει συνεχόμενα το ψηφίο της $i$ θέσης με το $2^{8-i}$. Εκμεταλλευόμενοι το γεγονός ότι το $2^{8-i}$ αναπαριστά τη δυαδική ακολουθία, μπορούμε να απλοποιήσουμε αυτή τη διαδικασία χρησιμοποιώντας τον τελεστή δυαδικής μετατόπισης προς τα αριστερά << που είναι διαθέσιμος σχεδόν σε όλες τις γλώσσες προγραμματισμού. Αυτό το κάνουμε για μεγαλύτερη ταχύτητα σε περιπτώσεις μαζικής επεξεργασίας και για απλοποίηση. Για παράδειγμα:

// n * Math.pow(2, 8)

> 3 * Math.pow(2, 8)
< 768

> 3 << 8
< 768

// δυαδικό   3 = 0000000011
// δυαδικό 768 = 1100000000 // μετατόπιση 8 θέσεων

Ο αλγόριθμός γραμμένος σε γλώσσα προγραμματισμού Javascript:

const afm = "090000045";
const sequence = afm.substring(0, 8);
let sum = 0;

for(let i = 0; i < 8; i++) {
  sum += parseInt(sequence[i]) << (8 - i);
}

const calc = sum % 11;
const d9 = parseInt(afm[8]);
const valid = calc % 10 === d9;

Για να ολοκληρώσουμε τη διαδικασία επαλήθευσης, πρέπει να ελέγξουμε λογικές παραμέτρους όπως εάν ο αριθμός αποτελείται από 9 αριθμητικούς μόνο χαρακτήρες και ο αριθμός δεν ισούται με μηδενικό "000000000".

Ολόκληρη ή διαδικασία απλοποιημένη σε γλώσσα προγραμματισμού Javascript:

function validateAFM(afm) {
  if(afm.length != 9) {
    // "Τα ψηφία του ΑΦΜ πρέπει να είναι 9 αριθμοί"
    return false;
  } 

  if(!/^\d+$/.test(afm)) {
    // "Αυτό που εισάγετε δεν είναι αριθμός"
    return false;
  }

  if(afm === '0'.repeat(9)) {
    // "Αυτό που εισάγετε είναι μηδενικός αριθμός (000000000)"
    return false;
  }

  const sum = afm
    .substring(0, 8)
    .split('')
    .reduce((s, v, i) => s + (parseInt(v) << (8 - i)), 0);

  const calc = sum % 11;
  const d9 = parseInt(afm[8]);
  const valid = calc % 10 === d9;

  return valid;
}

Παραγωγή

Αλγόριθμός παραγωγής

Για την παραγωγή νέων άκυρων αριθμών η διαδικασία μπορεί να είναι απλή και αφορά την παραγωγή 9 τυχαίων αριθμητικών ψηφίων, αλλά για το τελευταίο ψηφίο πρέπει να γίνει επαλήθευση και επαναπαραγωγή αν τυχαίνει να είναι έγκυρος. Για έγκυρους αριθμούς, θα πρέπει να υπολογίσουμε το άθροισμα των πρώτων 8 τυχαίων αριθμών και στη συνέχεια να υπολογίσουμε έγκυρο επαληθευτή για το τελευταίο ψηφίο. Μπορούμε να δημιουργήσουμε έναν βρόγχο που θα υπολογίζει το άθροισμα των πρώτον 8 τυχαίων ψηφίων, καθώς και θα δομεί την συνολική αλληλουχία συγκολλώντας το ένα τυχαίο ψηφίο μετά το άλλο. Στη συνέχεια υπολογίζουμε τον επαληθευτεί παίρνοντας το υπόλοιπο της διαίρεσης του αθροίσματος με το 11 και τέλος υπολογίζουμε το τελευταίο έγκυρο ψηφίο με το υπόλοιπο της διαίρεσης του επαληθευτή με το 10. Αν θέλουμε να δημιουργήσουμε άκυρο αριθμό, επαναλαμβάνουμε διαδικασία παραγωγής ενός τυχαίου αριθμού που να είναι διάφορός του έγκυρου αριθμού.

Ο μαθηματικός τύπος του αλγορίθμου δημιουργίας της αλληλουχίας τυχαίων ψηφίων, καθώς και του υπολογισμού του αθροίσματος:

$$\displaystyle\sum_{i=8}^{1} \substack{c = random(0, 9) \\ 2^{i}c \\ sequense \mathbin\Vert c}$$

Αυτό θα μας δώσει και την αλληλουχία τυχαίων ψηφίων αλλά και το άθροισμα τους, όπου στη συνέχεια μπορούμε να κάνουμε τους υπολογισμούς του τελευταίου ψηφίου.

Η διαδικασία παραγωγής σε γλώσσα προγραμματισμού Javascript:

function generateAFM(valid = true) {
  let body = '';
  let sum = 0;

  for(let i = 8; i >= 1; i--) {
    const digit = getRandomInt(0, 9);
    body += digit.toString();
    sum += digit << i;
  }

  const validator = sum % 11;
  const d9Valid = validator % 10;
  const d9 = valid ? d9Valid : getRandomInt(0, 9, d9Valid);

  return `${body}${d9}`;
}

// η συνάρτηση getRandomInt δέχεται 3 παραμέτρους; τον μικρότερο αριθμό (min), τον μεγαλύτερο αριθμό (max) και τον αριθμό που δεν επιθυμούμε να επιστρέψει (notEqual (optional))

// https://stackoverflow.com/a/1527820/1889685
function getRandomInt(min, max, notEqual = null) {
  let result;

  min = Math.ceil(min);
  max = Math.floor(max);

  do {
    result = Math.floor(Math.random() * (max - min + 1)) + min;
  } while(notEqual !== null && result === notEqual);

  return  result;
}

Προκειμένου να εξελίξουμε περαιτέρω τη διαδικασία, μπορούμε να προσθέσουμε δυνατότητες για συγκεκριμένες παραγωγές αριθμών, όπως παραγωγή μόνο αριθμών που να αντιστοιχούν σε φυσικά πρόσωπα (ξεκινάνε με 1 έως και 4) ή να έχουμε μη επαναλαμβανόμενα ψηφία (122344456).

Δυνατότητες γεννήτριας παραγωγής αριθμών μέσω παραμέτρων:

Εξαναγκασμός πρώτου ψηφίου (υπερκαλύπτει τα 2, 3, 4)
Μορφή παλαιότερη του 1999 (ξεκινάνε με τον αριθμό 0)
Μορφή για φυσικά πρόσωπα (ξεκινάει με ψηφίο 1-4)
Μορφή για νομικές οντότητες (ξεκινάει με ψηφίο 7-9)
Ανοχή επανάληψης ψηφίων (αφορά μόνο την αλληλουχία, όχι τον επαληθευτή)
Παραγωγή έγκυρου ή άκυρου αριθμού

Δείγμα των παραμέτρων της διαδικασίας παραγωγής σε γλώσσα προγραμματισμού Javascript:

/**
 * Generates an AFM number based on object parameters
 * @param {Object} [params={}] - Function parameters object. Empty object for all defaults.
 * @param {null|number} [params.forceFirstDigit] - If specified, overrides all pre99, legalEntity and individual.
 * @param {boolean} [params.pre99=false] - Για ΑΦΜ πριν από 1/1/1999 (ξεκινάει με 0), (if true, overrides both legalEntity and individual).
 * @param {boolean} [params.individual=false] - Φυσικά πρόσωπα, (ξεκινάει με 1-4)
 * @param {boolean} [params.legalEntity=false] - Νομικές οντότητες (ξεκινάει με 7-9)
 * @param {null|number} [params.repeatTolerance] - Number for max repeat tolerance (0 for no repeats, unspecified for no check)
 * @param {boolean} [params.valid=true] - Generate valid or invalid AFM
 * @returns {string} - A valid or invalid 9 digit AFM number
 */

export function generateAFM({
  forceFirstDigit,
  pre99 = false,
  individual = false,
  legalEntity = false,
  repeatTolerance,
  valid = true
} = {}) { ... }

Βιβλιοθήκες

LytraxAFM Sitribution Languages Η δικιά μου ανάγκη αφορούσε τη γλώσσα προγραμματισμού Java, θεώρησα όμως σωστό να δημιουργήσω βιβλιοθήκες για της 5 κυριότερες γλώσσες προγραμματισμού (Java, Javascript, PHP, Python, .Net (C#, VB.Net)) όπως και να ανεβάσω την κάθε βιβλιοθήκη στις αντίστοιχες βάσης δεδομένων διανομής για εύκολή πρόσβαση. Κάθε γλώσσα προγραμματισμού ή περιβάλλον έχει και το αντίστοιχο Github repository με οδηγίες εγκατάστασης, παραδείγματα και τεκμηρίωση API.

Δοκιμές (Unit testing)

Όλες οι κυκλοφορίες βιβλιοθηκών καλύπτονται από εκτεταμένες δοκιμές για ορθότητα λειτουργίας ούτως ώστε να εξασφαλίζεται η σωστή λειτουργία και της επαλήθευσης και της παραγωγής αριθμών. Μπορείτε να βρείτε οδηγίες για εκτέλεση των δοκιμαστικών μονάδων στο κάθε repository.

Επίλογος

Με αυτές τις βιβλιοθήκες πιστεύω ότι καλύπτεται ένα «κενό» σε κάτι που θεωρώ πολύ σημαντικό για όσους ασχολούνται με την ανάπτυξη λογισμικού και βρεθούνε σε αντίστοιχη θέση με μένα ή χρειάζονται αντίστοιχες λειτουργίες. Σχόλια για ενστάσεις, προτάσεις και συζήτηση είναι πάντα ευπρόσδεκτα.

Επαληθευτής και Γεννήτρια Αριθμών Φορολογικού Μητρώου

Βιβλιοθήκες για επαλήθευση και παραγωγή έγκυρων και άκυρων Αριθμών Φορολογικού Μητρώου